수학 공식 | 고등학교 > 쌍곡선의 뜻과 쌍곡선의 방정식
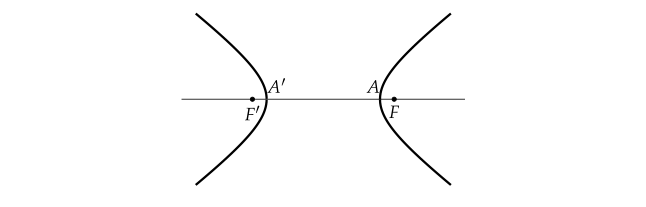
쌍곡선의 정의
- 평면 위의 두 정점 $ F $, $ F' $으로부터의 거리의 차가 일정한 점들의 집합을 쌍곡선이라 한다.
- 두 정점 $ F $, $ F' $을 잇는 직선이 쌍곡선과 만나는 점을 각각 $ A $, $ A' $이라 할 때, $ F $, $ F' $을 쌍곡선의 초점, $ A $, $ A' $을 쌍곡선의 꼭짓점, $ \overline{AA'} $을 쌍곡선의 주축, 주축의 중점을 쌍곡선의 중심이라 한다.
쌍곡선의 방정식
- 두 점 $ {F}(c, \ 0) $, $ {F'}(-c, \ 0) $으로부터의 거리의 차가 $ 2a $인 쌍곡선의 방정식
\begin{gather*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \ \ ( c > a > 0, \ \ b^2 = c^2-a^2)
\end{gather*} - 두 점 $ F(0, \ c) $, $ F'(0, \ -c) $로부터의 거리의 차가 $ 2b $인 쌍곡선의 방정식
\begin{gather*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = -1 \ \ ( c>b>0, \ \ a^2 = c^2-b^2)
\end{gather*}
- 두 점 $ (c, \ 0) $, $ (-c, \ 0) $으로부터의 거리의 차가 $ 2a $인 쌍곡선 위의 임의의 점을 $ (x, \ y) $라 하면 쌍곡선의 정의에 따라 다음 식이 성립한다. (단, $ c > a > 0 $)
\begin{gather*}
\left| \sqrt{(x-c)^2+y^2} - \sqrt{(x+c)^2+y^2} \right| = 2a \\
\therefore \ \sqrt{(x-c)^2+y^2} = \sqrt{(x+c)^2+y^2} \pm 2a
\end{gather*}양변을 제곱하여 정리하면
\begin{align*}
\pm a \sqrt{(x+c)^2+y^2} = a^2 + cx
\end{align*}이고, 다시 양변을 제곱하여 정리하면
\begin{align*}
(c^2-a^2) x^2 - a^2 y^2 = a^2 (c^2-a^2)
\end{align*}이다. $ c^2 - a^2 = b^2 \ (b>0) $으로 놓고 정리하면
\begin{align*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \ \ (\textrm{단}, \ b^2 = c^2-a^2)
\end{align*}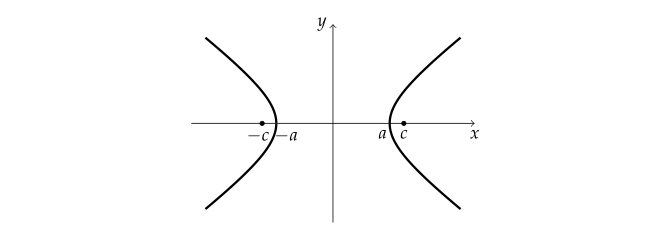
- 두 점 $ (0, \ c) $, $ (0, \ -c) $으로부터의 거리의 차가 $ 2b $인 쌍곡선 위의 임의의 점을 $ (x, \ y) $라 하면 쌍곡선의 정의에 따라 다음 식이 성립한다. (단, $ c > b > 0 $)
\begin{gather*}
\left| \sqrt{x^2+(y-c)^2} - \sqrt{x^2+(y+c)^2} \right| = 2b \\
\therefore \ \sqrt{x^2+(y-c)^2} = \sqrt{x^2+(y+c)^2} \pm 2b
\end{gather*}양변을 제곱하여 정리하면
\begin{align*}
\pm b \sqrt{x^2+(y+c)^2} = b^2 + cy
\end{align*}이고, 다시 양변을 제곱하여 정리하면
\begin{align*}
b^2 x^2 - ( c^2 - b^2 ) y^2 = - b^2 (c^2-b^2)
\end{align*}이다. $ c^2 - b^2 = a^2 \ (a>0) $으로 놓고 정리하면
\begin{align*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = - 1 \ \ (\textrm{단}, \ a^2 = c^2-b^2)
\end{align*}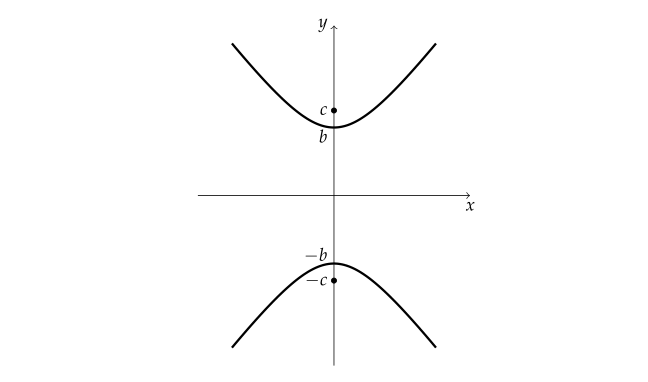
두 점 $ (5, \ 0) $, $ (-5, \ 0) $으로부터의 거리의 차가 $ 6 $인 쌍곡선의 방정식을 구하여라.
$ c = 5 $, $ a = 3 $이므로 $ b^2 = 25-9 = 16 $이다. 따라서
\begin{gather*}
\frac{x^2}{9} - \frac{y^2}{16} = 1
\end{gather*}
두 점 $ (0, \ 4) $, $ (0, \ -4) $으로부터의 거리의 차가 $ 6 $인 쌍곡선의 방정식을 구하여라.
$ c = 4 $, $ b = 3 $이므로 $ a^2 = 16-9 = 7 $이다. 따라서
\begin{gather*}
\frac{x^2}{7} - \frac{y^2}{9} = -1
\end{gather*}
쌍곡선의 점근선
쌍곡선
\begin{gather*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \ \ (a>0, \ b>0)
\end{gather*}
의 점근선의 방정식은
\begin{gather*}
y = \pm \frac{b}{a} x
\end{gather*}
쌍곡선 $ \dfrac{x^2}{a^2} - \dfrac{y^2}{b^2} = \pm 1 $을 $ y $에 관하여 풀면
\begin{align*}
y &= \pm \frac{b}{a} \sqrt{x^2-a^2} = \pm \frac{b}{a} \sqrt{x^2 \left( 1 \mp \frac{a^2}{x^2} \right)} \\
&= \pm \frac{b}{a} x \sqrt{\left( 1 \mp \frac{a^2}{x^2} \right)}
\end{align*}
이고,
\begin{align*}
\lim_{x \rightarrow \infty} \pm \frac{b}{a} x \sqrt{\left( 1 \mp \frac{a^2}{x^2} \right)} &= \lim_{x \rightarrow -\infty} \pm \frac{b}{a} x \sqrt{\left( 1 \mp \frac{a^2}{x^2} \right)} \\
&= \pm \frac{b}{a} x
\end{align*}
이다. 따라서 쌍곡선은 $ x $가 원점에서 멀어질수록
\begin{align*}
y= \pm \frac{b}{a}x
\end{align*}
에 가까워지는데, 이를 쌍곡선의 점근선이라 한다.
쌍곡선의 평행이동
쌍곡선
\begin{gather*}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = \pm 1 \ \ (a>0, \ b>0)
\end{gather*}
을 $ x $축 방향으로 $ m $, $ y $축 방향으로 $ n $만큼 평행이동시킨 쌍곡선의 방정식은
\begin{gather*}
\frac{(x-m)^2}{a^2} - \frac{(y-n)^2}{b^2} = \pm 1
\end{gather*}
쌍곡선의 방정식의 일반형
평행이동한 쌍곡선의 방정식을 전개하면
\begin{gather*}
Ax^2 + By^2 + Cx + Dy + E = 0 \ \ (\textrm{단}, \ AB<0)
\end{gather*}