수학 공식 | 고등학교 > 두 점 사이의 거리
수직선 위의 두 점 사이의 거리
- 수직선 위의 두 점 $ {A}(x_1) $, $ {B}(x_2) $ 사이의 거리 $ \overline{AB} $는
\begin{align*}
\overline{AB} = |x_2 - x_1|
\end{align*} - 원점 $ O $와 점 $ {A}(x_1) $ 사이의 거리 $ \overline{OA} $는
\begin{align*}
\overline{OA} = |x_1|
\end{align*}
좌표평면 위의 두 점 사이의 거리
- 좌표평면 위의 두 점 $ {A}(x_1, \ y_1) $, $ {B}(x_2, \ y_2) $ 사이의 거리 $ \overline{AB} $는
\begin{align*}
\overline{AB} = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}
\end{align*} - 원점 $ O $와 점 $ {A}(x_1, \ y_1) $ 사이의 거리 $ \overline{OA} $는
\begin{align*}
\overline{OA} = \sqrt{{x_1}^2 + {y_1}^2}
\end{align*}
파푸스의 중선정리
삼각형 $ {ABC} $에서 변 $ {BC} $의 중점을 $ {M} $이라 할 때
\begin{gather*}
{\overline{AB}^2+\overline{AC}^2=2(\overline{AM}^2+\overline{BM}^2)}
\end{gather*}
이 성립한다. 이를 파푸스의 중선정리(Pappus's Centroid Theorem) 또는 아폴로니오스의 정리(Apollonius' Theorem)라고 한다.
좌표평면 위에 점 $ {B} $와 $ {C} $는 $ x $축 위에 놓고, 변 $ {BC} $의 중점 $ {M} $을 원점으로 한다. 그리고, 각 점의 좌표를 $ {A}(a, \ b) $, $ {B}(-c, \ 0) $, $ {C}(c, \ 0) $, $ {M}(0, \ 0) $로 놓는다.
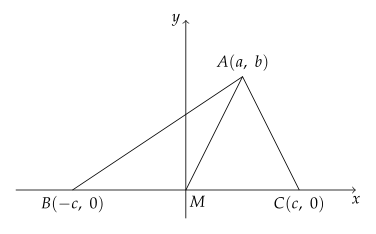
중선정리의 좌변 $ {\overline{AB}^2+\overline{AC}^2} $은 다음과 같이 정리된다.
\begin{gather*}
{\overline{AB}^2+\overline{AC}^2} = \{ (a+c)^2+b^2 \} + \{ (a-c)^2+b^2 \} =2a^2+2b^2+2c^2
\end{gather*}
중선정리의 우변 $ {2(\overline{AM}^2+\overline{BM}^2)} $은 다음과 같이 정리된다.
\begin{gather*}
{2(\overline{AM}^2+\overline{BM}^2)}=2(a^2+b^2+c^2) = 2a^2+2b^2+2c^2
\end{gather*}
따라서
\begin{gather*}
{\overline{AB}^2+\overline{AC}^2=2(\overline{AM}^2+\overline{BM}^2)}
\end{gather*}
이 성립한다.
잡동사니
- 좌표평면 위의 세 점 $ A $, $ B $, $ C $로부터 같은 거리에 있는 점은 삼각형 $ ABC $의 외심이다.
- 좌표평면 위의 두 점 $ A $, $ B $에 대하여 $ \overline{PA} + \overline{PB} $를 최소로 만드는 점 $ P $는 선분 $ AB $ 위의 점이다.
- 좌표평면 위의 두 점 $ A $, $ B $에 대하여 $ \overline{PA}^2 + \overline{PB}^2 $를 최소로 만드는 점 $ P $는 선분 $ AB $의 중점이다.