수학 공식 | 고등학교 > 두 직선의 평행 조건과 수직 조건
두 직선의 평행과 수직 - $ \boldsymbol{ y = mx + n } $의 꼴
두 직선 $ y=mx+n $, $ y=m'x+n' $에 대하여
- 두 직선이 서로 평행하다. $ \Longleftrightarrow \ \ m = m', \ n \neq n' $
- 두 직선이 서로 수직이다. $ \Longleftrightarrow \ \ m m' = -1 $
두 직선 $ y=mx+n $, $ y=m'x+n' $이 서로 수직이면 두 직선 $ y=mx $, $ y=m'x $도 서로 수직이다.
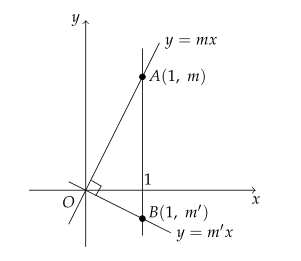
수직인 두 직선 $ y=mx $, $ y=m'x $와 직선 $ x=1 $의 교점을 각각 $ A $, $ B $라 하면
\begin{gather*}
\overline{AB}^2 = \overline{OA}^2 + \overline{OB}^2
\end{gather*}
이고, 두 점 $ A $, $ B $의 좌표는 $ A(1, \ m) $, $ B(1, \ m') $이므로
\begin{gather*}
( m-m' )^2 = ( 1+m^2 ) + \{ 1+(m')^2 \} \ \ \ \therefore \ \ mm' = -1
\end{gather*}
두 직선의 평행과 수직 - $ \boldsymbol{ ax+by+c=0 } $의 꼴
두 직선 $ ax+by+c=0 $, $ a'x+b'y+c'=0 $에 대하여
- 두 직선이 서로 평행하다. $ \Longleftrightarrow \ \ \dfrac{a}{a'} = \dfrac{b}{b'} \neq \dfrac{c}{c'} $
- 두 직선이 서로 수직이다. $ \Longleftrightarrow \ \ aa' + bb' = 0 $
직선 $ ax+by+c=0 $의 기울기는 $ - \dfrac{a}{b} $, $ y $절편은 $ -\dfrac{c}{b} $이고, 직선 $ a'x+b'y+c'=0 $의 기울기는 $ - \dfrac{a'}{b'} $, $ y $절편은 $ -\dfrac{c'}{b'} $이다.
- 두 직선이 서로 평행하기 위해서는 기울기가 같고 $ y $절편이 달라야 하므로
\begin{gather*}
- \dfrac{a}{b} = - \dfrac{a'}{b'}, \ \ -\dfrac{c}{b} \neq -\dfrac{c'}{b'} \ \ \ \therefore \ \ \dfrac{a}{a'} = \dfrac{b}{b'} \neq \dfrac{c}{c'}
\end{gather*} - 두 직선이 서로 수직이기 위해서는 기울기의 곱이 $ -1 $이어야 하므로
\begin{gather*}
\left( - \dfrac{a}{b} \right) \times \left( - \dfrac{a'}{b'} \right) = -1 \ \ \ \therefore \ \ aa' + bb' = 0
\end{gather*}
2018/06/08 11:56수학 공식