수학 공식 | 고등학교 > 삼차방정식과 사차방정식
삼차방정식과 사차방정식
다항식 $ f(x) $가 $ x $에 대한 삼차식이면 방정식 $ f(x) = 0 $은 $ x $에 대한 삼차방정식이라 하고, $ x $에 대한 사차식이면 방정식 $ f(x) = 0 $은 $ x $에 대한 사차방정식이라 한다.
삼차방정식과 사차방정식의 풀이
인수분해 공식과 인수정리를 이용하여 인수분해한 후 해를 구한다.
다음 방정식을 풀어라.
\begin{gather*}
x^3 + 1 = 0
\end{gather*}
좌변을 인수분해하면 $ (x+1)(x^2 - x + 1)=0 $이므로
\begin{gather*}
x+1 = 0 \ \ \textrm{또는} \ \ x^2 - x + 1 = 0
\end{gather*}
따라서 근은 $ x=-1 $ 또는 $ x = \dfrac{1+\sqrt{3}i}{2} $이다.
다음 방정식을 풀어라.
\begin{gather*}
x^3 - 7x + 6 = 0
\end{gather*}
$ x=1 $을 대입하면 $ 0 $이므로
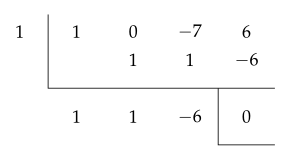
$ (x-1)(x^2 + x - 6) = 0 \ \ \ \therefore \ \ (x-1)(x-2)(x+3)=0 $
따라서 근은 $ x=1 $ 또는 $ x=2 $ 또는 $ x=-3 $이다.
삼차방정식 $ \boldsymbol{ x^3 - 1 = 0 } $의 허근의 성질
삼차방정식 $ x^3 - 1 = 0 $의 한 허근을 $ \omega $라 하면
- $ \omega^3 = 1 $, $ \omega^2 + \omega + 1 = 0 $
- $ \overline{\omega}^3 = 1 $, $ \overline{\omega}^2 + \overline{\omega} + 1 = 0 $
- $ \omega + \overline{\omega} = -1 $, $ \omega \overline{\omega} = 1 $
좌변을 인수분해하면 $ ( x - 1 )( x^2 + x + 1 ) = 0 $
- $ \omega $는 $ x^3 - 1 = 0 $의 근이므로 $ \omega^3 - 1 = 0 $
$ \omega $는 $ x^2 + x + 1 = 0 $의 근이므로 $ \omega^2 + \omega + 1 = 0 $ - 계수가 실수이므로 $ \omega $가 근이면 $ \overline{\omega} $도 근이다.
- $ x^2 + x + 1 = 0 $의 근이 $ \omega $와 $ \overline{\omega} $이므로, 근과 계수의 관계에 의하여
$ \omega + \overline{\omega} = -1, \ \ \omega \overline{\omega} = 1 $
삼차방정식 $ \boldsymbol{ x^3 + 1 = 0 } $의 허근의 성질
삼차방정식 $ x^3 + 1 = 0 $의 한 허근을 $ \omega $라 하면
- $ \omega^3 = -1 $, $ \omega^2 - \omega + 1 = 0 $
- $ \overline{\omega}^3 = -1 $, $ \overline{\omega}^2 - \overline{\omega} + 1 = 0 $
- $ \omega + \overline{\omega} = 1 $, $ \omega \overline{\omega} = 1 $
좌변을 인수분해하면 $ ( x + 1 )( x^2 - x + 1 ) = 0 $
- $ \omega $는 $ x^3 + 1 = 0 $의 근이므로 $ \omega^3 + 1 = 0 $
$ \omega $는 $ x^2 - x + 1 = 0 $의 근이므로 $ \omega^2 - \omega + 1 = 0 $ - 계수가 실수이므로 $ \omega $가 근이면 $ \overline{\omega} $도 근이다.
- $ x^2 - x + 1 = 0 $의 근이 $ \omega $와 $ \overline{\omega} $이므로, 근과 계수의 관계에 의하여
$ \omega + \overline{\omega} = 1, \ \ \omega \overline{\omega} = 1 $
방정식 $ x^3 - 1 = 0 $의 한 허근을 $ \omega $라 할 때
\begin{gather*}
\omega^{100} + \omega^{101} + \omega^{102}
\end{gather*}
의 값을 구하여라.
$ \omega^{3} = 1 $이므로
\begin{gather*}
(\omega^{3})^{33} \omega + (\omega^{3})^{33} \omega^2 + (\omega^{3})^{34} = \omega + \omega^2 + 1
\end{gather*}
$ \omega^2 + \omega + 1 = 0 $이므로 정답은 $ 0 $이다.
삼차방정식의 근과 계수의 관계
$ x $에 대한 삼차방정식 $ ax^3 + bx^2 + cx + d = 0 $의 세 근을 $ \alpha $, $ \beta $, $ \gamma $라 할 때
\begin{gather*}
\alpha + \beta + \gamma = - \frac{b}{a}, \ \ \alpha \beta + \beta \gamma + \gamma \alpha = \frac{c}{a}, \ \ \alpha \beta \gamma = - \frac{d}{a}
\end{gather*}