수학 공식 | 고등학교 > 인수분해
인수분해
하나의 다항식을 두 개 이상의 다항식의 곱으로 나타내는 것을 인수분해라 하고, 곱을 이루는 각각의 다항식을 그 다항식의 인수라 한다.
인수분해 공식
- $ a^2 + 2ab + b^2 = (a+b)^2 $
- $ a^2 - 2ab + b^2 = (a-b)^2 $
- $ a^2-b^2 = (a+b)(a-b) $
- $ x^2 + (a+b)x + ab = (x+a)(x+b) $
- $ acx^2 + (ad+bc)x + bd = (ax+b)(cx+d) $
- $ x^3 + (a+b+c)x^2 + (ab+bc+ca)x + abc \\= (x+a)(x+b)(x+c) $
- $ a^2+b^2+c^2+2ab+2bc+2ca = (a+b+c)^2 $
- $ a^3 + 3a^2b + 3ab^2 + b^3 = (a+b)^3 $
- $ a^3 - 3a^2b + 3ab^2 - b^3 = (a-b)^3 $
- $ a^3+b^3 = (a+b)(a^2-ab+b^2) $
- $ a^3-b^3 = (a-b)(a^2+ab+b^2) $
- $ a^3+b^3+c^3-3abc \\= (a+b+c)(a^2+b^2+c^2-ab-bc-ca) $
- $ a^4+a^2b^2+b^4 = (a^2+ab+b^2)(a^2-ab+b^2) $
인수분해 방법
- 공통인수가 있으면 묶는다.
- 인수분해 공식을 이용하여 인수분해한다.
- 공통부분이 있으면 치환한다.
- 복이차식인 경우 치환하거나 $ A^2 - B^2 $의 꼴로 변형한다.
- 여러 개의 문자를 포함한 경우 차수가 낮은 문자에 대하여 내림차순으로 정리한다.
- 삼차 이상의 식인 경우 인수정리를 이용한다.
다음 식을 인수분해하여라.
- $ x^4 - 3x^2 - 4 $
- $ x^4 + 3x^2 + 4 $
- $ x^2 = X $로 치환하여 인수분해한다.
\begin{align*}
X^2 - 3X - 4 &= (X-4)(X+1) = (x^2 - 4)(x^2 + 1) \\
&= (x+2)(x-2)(x^2+1)
\end{align*} - $ A^2 - B^2 $의 꼴로 변형하여 인수분해한다.
\begin{align*}
x^4 + 4x^2 + 4 - x^2 &= (x^2+2)^2 - x^2 \\
&= (x^2 + 2 + x)(x^2 + 2 - x) \\
&= (x^2 + x + 2)(x^2 - x + 2)
\end{align*}
다음 식을 인수분해하여라.
\begin{gather*}
x^2+3xy+2y^2-x-3y-2
\end{gather*}
$ x $에 대하여 내림차순으로 정리한 후 인수분해한다.
\begin{align*}
& x^2 + (3y-1)x + 2y^2 - 3y - 2 \\
& = x^2 + (3y-1)x + (y-2)(2y+1) \\
& = (x+y-2)(x+2y+1)
\end{align*}
다음 식을 인수분해하여라.
\begin{gather*}
x^3 - 6x^2 + 11x - 6
\end{gather*}
$ x=1 $을 대입하면 $ 0 $이므로 $ x-1 $을 인수로 가진다.
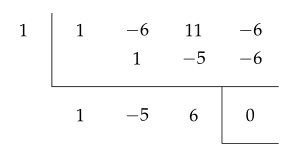
$ (x-1)(x^2 - 5x + 6) = (x-1)(x-2)(x-3) $
2018/02/01 12:54수학 공식