수학 공식 | 고등학교 > 도함수의 활용 - 방정식과 부등식
방정식에의 활용
- 방정식 $ f(x) = 0 $의 실근의 개수
⇨ 함수 $ y=f(x) $의 그래프와 $ x $축의 교점의 개수 - 방정식 $ f(x) = g(x) $의 실근의 개수
⇨ 함수 $ y=f(x) $의 그래프와 함수 $ y=g(x) $의 그래프의 교점의 개수
방정식 함수 $ x^3 - 12x - a = 0 $의 근이 다음과 같도록 실수 $a$의 값 또는 범위를 구하여라.
- 서로 다른 세 실근
- 서로 다른 두 실근
- 한 실근
- 서로 다른 두 개의 음의 근과 한 개의 양의 근
$ x^3 - 12x = a $이므로 방정식의 실근은 함수 $ y = x^3 - 12x $와 $ y = a $의 교점의 $ x $좌표와 같다.
$ f(x) = x^3 - 12x $하면 $ f'(x) = 3(x+2)(x-2) $이므로
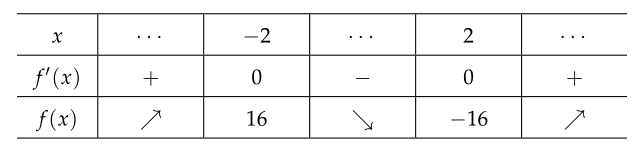
$ y = f(x) $와 $ y=a $의 그래프는 다음과 같고, $ a $의 값에 따라 실근의 개수가 달라진다.
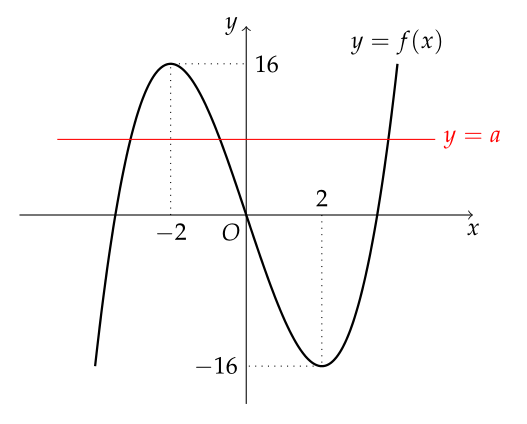
- $ -16 < a < 16 $
- $ a=-16 $ 또는 $ a=16 $
- $ a < -16 $ 또는 $ a > 16 $
- $ 0 < a < 16 $
부등식에의 활용
- 모든 실수 $ x $에 대하여 $ f(x) > 0 $의 증명
⇨ ($ f(x) $의 최솟값) $ > 0 $임을 보인다. - $ x>a $인 범위에서 $ f(x) > 0 $의 증명
⇨ $ x>a $에서 ($ f(x) $의 최솟값) $ > 0 $임을 보인다.
⇨ $ x>a $에서 $ f(x) $가 증가하고 $ f(a) \geq 0 $임을 보인다.
- $ f(x) > g(x) $의 증명은 $ h(x) = f(x) - g(x) $로 놓고 위 방법을 이용한다.
부등식 $ x^4 - 4x + a \geq 0 $이 항상 성립하도록 하는 상수 $ a $의 값의 범위를 구하여라.
$ f(x) = x^4 - 4x + a $라 하면
\begin{gather*}
f'(x) = 4(x-1)(x^2 + x + 1)
\end{gather*}
이고 $ x=1 $에서 최솟값을 가진다.
\begin{gather*}
f(1) \geq 0 \ \ \ \therefore \ \ a \geq 3
\end{gather*}
$ x > 2 $일 때 부등식 $ x^3 - 3x + a > 0 $이 성립하도록 하는 상수 $ a $의 값의 범위를 구하여라.
$ f(x) = x^3 - 3x + a $라 하면
\begin{gather*}
f'(x) = 3(x+1)(x-1)
\end{gather*}
이고, $ x>1 $에서 $ f(x) $는 증가한다.
부등식이 성립하기 위해서는 $ f(2) \geq 0 $이면 되므로
\begin{gather*}
f(2) = 8-6+a \geq 0 \ \ \ \therefore \ \ a \geq -2
\end{gather*}