수학 공식 | 고등학교 > 이차함수의 최대, 최소
이차함수의 최대, 최소 1
정의역이 실수 전체의 집합인 경우 이차함수 $ y = a (x-p)^2 + q $의 최댓값과 최솟값은 다음과 같다.
- $ a > 0 $일 때 최댓값은 없고 최솟값은 $ q $이다.
- $ a < 0 $일 때 최댓값은 $ q $이고 최솟값은 없다.
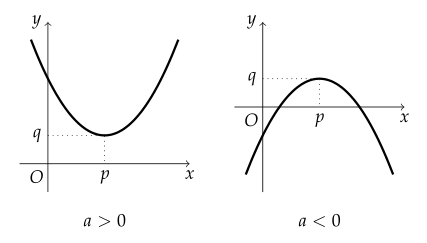
이차함수의 최대, 최소 2
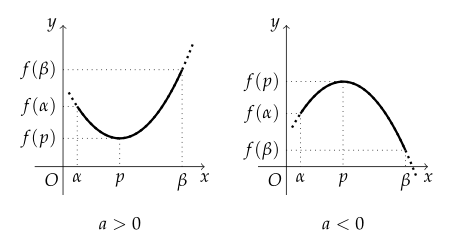
정의역이 $ \{ x | \alpha \leq x \leq \beta \} $인 경우 이차함수 $ y = a (x-p)^2 + q $의 최댓값과 최솟값은 다음과 같다.
꼭짓점의 $ x $좌표가 $ \alpha \leq x \leq \beta $에 포함되는 경우 $ f(\alpha) $, $ f(p) $, $ f(\beta) $ 중 가장 큰 값이 최댓값, 가장 작은 값이 최솟값이다.
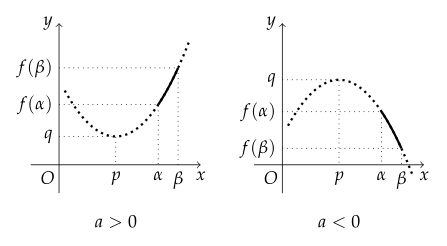
꼭짓점의 $ x $좌표가 $ \alpha \leq x \leq \beta $에 포함되지 않는 경우 $ f(\alpha) $, $ f(\beta) $ 중 큰 값이 최댓값, 작은 값이 최솟값이다.
이차함수 $ y = x^2 - 2x + 2 $에 대하여 다음 물음에 답하여라.
- 정의역이 실수 전체의 집합일 때 최댓값 또는 최솟값을 구하여라.
- $ 0 \leq x \leq 3 $일 때 최댓값과 최솟값을 구하여라.
- $ 2 \leq x \leq 3 $일 때 최댓값과 최솟값을 구하여라.
$ y = x^2 - 2x + 2 = (x-1)^2 + 1 $이므로 꼭짓점의 $ x $좌표는 $ 1 $이다.
- 이차항의 계수가 양수이므로 최솟값은 $ 1 $이다.
- $ f(0) = 2 $, $ f(1) = 1 $, $ f(3) = 5 $이므로 최댓값은 $ 5 $, 최솟값은 $ 1 $이다.
- $ f(2) = 2 $, $ f(3) = 5 $이므로 최댓값은 $ 5 $, 최솟값은 $ 2 $이다.
2018/06/17 09:38수학 공식