수학 공식 | 고등학교 > 이차함수의 그래프와 직선의 위치 관계
이차함수의 그래프와 직선의 위치 관계
- 이차함수 $ y = ax^2 + bx +c $의 그래프와 직선 $ y = mx + n $의 교점의 $ x $좌표는 이차방정식
\begin{gather*}
ax^2 + (b-m)x + c-n = 0
\end{gather*}의 실근과 같다. - 이차방정식 $ ax^2 + (b-m)x + c-n = 0 $의 판별식 $ D $에 대하여
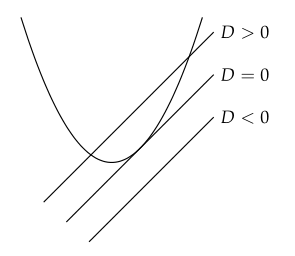
$ D > 0 $이면 서로 다른 두 실근을 갖고, 이차함수는 직선과 서로 다른 두 점에서 만난다.
$ D = 0 $이면 중근을 갖고, 이차함수는 직선과 한 점에서 만난다(접한다).
$ D < 0 $이면 실근을 갖지 않고, 이차함수는 직선과 만나지 않는다.
이차함수 $ y = -x^2 - 2x - a $의 그래프가 직선 $ y = 2x - 1 $과 만나도록 하는 실수 $ a $의 값의 범위를 구하여라.
$ -x^2 - 2x - a = 2x - 1 \ \ \ \therefore \ \ x^2 + 4x + a - 1 = 0 $
$ D/4 = 2^2 - (a-1) \geq 0 \ \ \ \therefore \ \ a \leq 5 $
2018/06/17 09:28수학 공식