수학 공식 | 고등학교 > 평균변화율과 미분계수
평균변화율
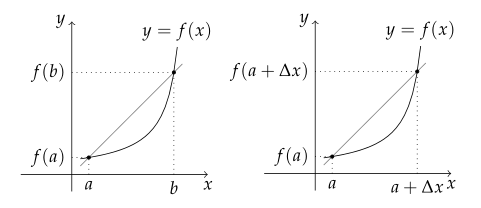
함수 $ y = f(x) $에서 $ x $의 값이 $ a $에서 $ b $까지 변할 때의 평균변화율은
\begin{gather*}
\frac{\Delta y}{\Delta x} = \frac{f(b) - f(a)}{b-a} = \frac{f(a+\Delta x) - f(a)}{\Delta x}
\end{gather*}
평균변화율의 기하학적 의미
평균변화율은 $ ( a, \ f(a) ) $, $ ( b, \ f(b) ) $를 잇는 직선의 기울기와 같다.
미분계수
함수 $ y = f(x) $의 $ x=a $에서의 미분계수는
\begin{gather*}
f'(a) = \lim_{h \rightarrow 0} \frac{f(a+h) - f(a)}{h} = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x-a}
\end{gather*}
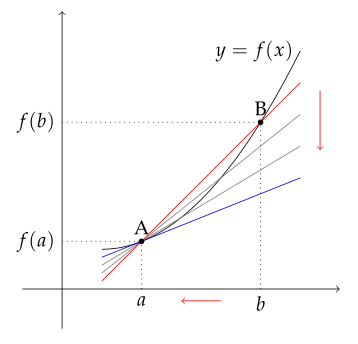
미분계수의 기하학적 의미
미분계수 $ f'(a) $는 $ ( a, \ f(a) ) $에서의 접선의 기울기와 같다.
이차함수 $ f(x) = x^2 $에서 $ x $의 값이 $ 1 $에서 $ 3 $까지 변할 때의 평균변화율과 $ x=a $에서의 미분계수는 같다. 상수 $ k $의 값을 구하여라.
평균변화율은
\begin{gather*}
\frac{3^2 - 1^2}{3-1} = 4
\end{gather*}
$ x=a $에서 미분계수는
\begin{gather*}
f'(a) = \lim_{h \to 0} \frac{(a+h)^2 - a^2}{h} = 2a
\end{gather*}
두 값이 같아야 하므로
\begin{gather*}
2a = 4 \ \ \ \therefore \ \ a=2
\end{gather*}
잡동사니
이차함수에서 $ x $의 값이 $ \alpha $에서 $ \beta $까지 변할 때의 평균변화율과 같은 값의 미분계수를 만드는 $ x $의 값은 $ \alpha $와 $ \beta $의 산술평균
\begin{gather*}
\frac{\alpha + \beta}{2}
\end{gather*}
이다.