MATH FACTORY

1. 내분점

$ {A}(x_1) $, $ {B}(x_2) $, $ x_1 < x_2 $일 때 선분 $ {AB} $를 $ m:n $ ($ m>0 $, $ n>0 $)으로 내분하는 점을 $ P(x) $라 하자.

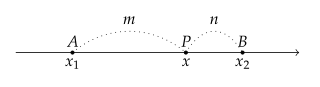
$ \overline{AP}=x-x_1 $, $ \overline{PB}=x_2-x $이므로, 점 $ P $의 좌표는

\begin{align*}
(x-x_1):(x_2-x)=m:n \ \ \ \therefore \ \ x=\frac{mx_2+nx_1}{m+n}
\end{align*}

같은 방법으로 하면 $ x_1 > x_2 $일 때도 결과는 같다.

2. 외분점

$ {A}(x_1) $, $ {B}(x_2) $, $ x_1 < x_2 $일 때 선분 $ {AB} $를 $ m:n $ ($ m>0 $, $ n>0 $, $ m \neq n $)으로 외분하는 점을 $ {Q}(x) $라 하자.

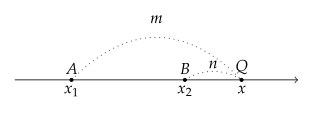
$ m > n $일 때 $ \overline{AQ}=x-x_1 $, $ \overline{BQ}=x-x_2 $이므로, 점 $ {Q} $의 좌표는

\begin{align*}
(x-x_1):(x-x_2)=m:n \ \ \ \therefore \ \ x=\frac{mx_2-nx_1}{m-n}
\end{align*}

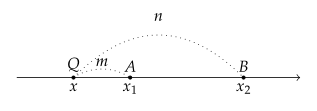
$ m < n $일 때 $ \overline{AQ}=x_1-x $, $ \overline{BQ}=x_2-x $이므로, 점 $ {Q} $의 좌표는

\begin{align*}
(x_1-x):(x_2-x)=m:n \ \ \ \therefore \ \ x=\frac{mx_2-nx_1}{m-n}
\end{align*}

같은 방법으로 하면 $ x_1 > x_2 $일 때도 결과는 같다.

3. 중점

내분점에서 $ m=n $일 때의 점 $ {P} $를 선분 $ {AB} $의 중점이라고 한다.

\begin{align*}
x=\frac{mx_2+nx_1}{m+n}=\frac{mx_2+mx_1}{m+m} = \frac{x_1+x_2}{2}
\end{align*}

좌표평면 위의 두 점 $ {A}(x_1, \ y_1) $, $ {B}(x_2, \ y_2) $의 $ m:n $ 내분점을 $ {P}(x, \ y) $라 하고, 각 점에서 $ x $축에 내린 수선의 발을 각각 $ {A'} $, $ {P'} $, $ {B'} $라고 하자.

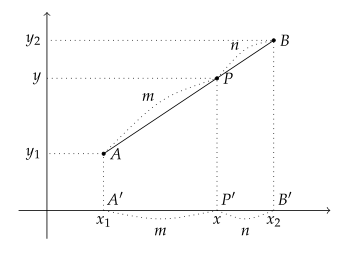
$ \overline{AP} : \overline{PB} $가 $ m:n $이면 $ \overline{A'P'} : \overline{P'B'} $도 $ m:n $이다. 따라서 선분 $ AB $의 $ m:n $ 내분점의 $ x $좌표는 점 $ A $의 $ x $좌표와 점 $ B $의 $ x $좌표의 $ m:n $ 내분점의 좌표와 같다.

마찬가지로 선분 $ AB $의 $ m:n $ 내분점의 $ y $좌표는 점 $ A $의 $ y $좌표와 점 $ B $의 $ y $좌표의 $ m:n $ 내분점의 좌표와 같다.

외분점의 좌표와 중점의 좌표도 같은 방식으로 구한다. 즉, $ x $좌표는 $ x $좌표끼리, $ y $좌표는 $ y $좌표끼리 계산한다.

삼각형의 무게중심은 중선을 $ 2:1 $로 내분하는 점이다.

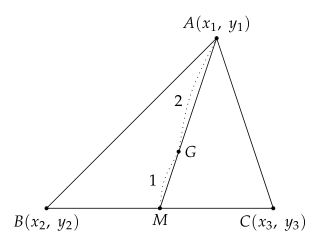
위와 같은 삼각형 $ {ABC} $가 있다고 할 때, 변 $ {BC} $의 중점 $ {M} $의 좌표는

\begin{gather*}
{M} \left( \frac{x_2 + x_3}{2}, \ \frac{y_2 + y_3}{2} \right)
\end{gather*}

무게중심 $ {G} $는 중선 $ {AM} $의 $ 2:1 $ 내분점이므로 점 $ {G} $의 $ x $좌표는

\begin{gather*}
\frac{2 \times \dfrac{x_2 + x_3}{2} + 1 \times x_1}{2+1} = \frac{x_1 + x_2 + x_3}{3}
\end{gather*}

무게중심의 $ y $좌표도 같은 방법으로 구할 수 있다. 따라서, 세 점 $ {A}(x_1 \ y_1) $, $ {B}(x_2 \ y_2) $, $ {C}(x_3 \ y_3) $을 꼭짓점으로 하는 삼각형의 무게중심 $ {G} $의 좌표는

\begin{gather*}
{G} \left( \frac{x_1 + x_2 + x_3}{3}, \ \frac{y_1 + y_2 + y_3}{3} \right)
\end{gather*}