수학 공식 | 고등학교 > 삼각함수의 덧셈정리
여러 가지 삼각함수
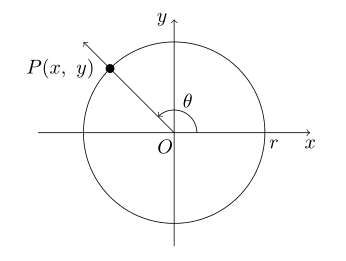
좌표평면 위에서 $ x $축의 양의 부분을 시초선, 일반각 $ \theta $의 동경을 $ OP $라고 하자. 반지름의 길이가 $ r $인 원 위의 점 $ P(x, \ y) $에 대하여
\begin{gather*}
\frac{r}{y}, \ \ \frac{r}{x}, \ \ \frac{x}{y} \ (y \neq 0)
\end{gather*}
의 값은 $ r $에 관계없이 $ \theta $의 값에 따라 각각 하나씩 결정되는 $ \theta $에 대한 함수이다. 이 함수를 각각 $ \theta $에 대한 코시컨트함수, 시컨트함수, 코탄젠트함수라 하고 다음과 같이 나타낸다.
\begin{gather*}
\csc \theta = \frac{r}{y}, \ \ \sec \theta = \frac{r}{x}, \ \ \cot \theta = \frac{x}{y}
\end{gather*}
여러 가지 삼각함수 사이의 관계
- $ \csc \theta = \dfrac{1}{\sin \theta}, \ \ \sec \theta = \dfrac{1}{\cos \theta}, \ \ \cot \theta = \dfrac{1}{\tan \theta} $
- $ 1 + \tan^2 \theta = \sec^2 \theta, \ \ 1 + \cot^2 \theta = \csc^2 \theta $
2의 증명
$ 1 + \tan^2 \theta = 1 + \dfrac{\sin^2 \theta}{\cos^2 \theta} = \dfrac{\cos^2 \theta + \sin^2 \theta}{\cos^2 \theta} = \dfrac{1}{\cos^2 \theta} = \sec^2 \theta $
$ 1 + \cot^2 \theta = 1 + \dfrac{\cos^2 \theta}{\sin^2 \theta} = \dfrac{\sin^2 \theta + \cos^2 \theta}{\sin^2 \theta} = \dfrac{1}{\sin^2 \theta} = \csc^2 \theta $
삼각함수의 덧셈정리
- $ \sin (\alpha+\beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta $
- $ \sin (\alpha-\beta) = \sin \alpha \cos \beta - \cos \alpha \sin \beta $
- $ \cos (\alpha+\beta) = \cos \alpha \cos \beta - \sin \alpha \sin \beta $
- $ \cos (\alpha-\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta $
- $ \displaystyle \tan(\alpha+\beta) = \frac{\tan \alpha + \tan \beta}{1-\tan \alpha \tan \beta} $
- $ \displaystyle \tan(\alpha-\beta) = \frac{\tan \alpha - \tan \beta}{1+\tan \alpha \tan \beta} $
다음 값을 구하여라.
- $ \sin 75^\circ $
- $ \sin 15^\circ $
- $ \cos 80^\circ \cos 40^\circ - \sin 80^\circ \sin 40^\circ $
- $ \cos 110^\circ \cos 65^\circ + \sin 110^\circ \sin 65^\circ $
- $ \sin 75^\circ = \sin( 45^\circ + 30^\circ ) = \dfrac{\sqrt{6} + \sqrt{2}}{4} $
- $ \sin 15^\circ = \sin( 45^\circ - 30^\circ ) = \dfrac{\sqrt{6} - \sqrt{2}}{4} $
- $ \cos(80^\circ + 40^\circ) = -\dfrac{1}{2} $
- $ \cos(110^\circ - 65^\circ) = \dfrac{\sqrt{2}}{2} $
삼각함수의 덧셈정리의 응용
- $ \sin 2\alpha = 2 \sin \alpha \cos \alpha $
- $ \cos 2\alpha = \cos^2 \alpha - \sin^2 \alpha = 2 \cos^2 \alpha -1 = 1-2 \sin^2 \alpha $
- $ \displaystyle \tan 2\alpha = \frac{2 \tan \alpha}{1-\tan^2 \alpha} $
- $ \displaystyle \sin^2 \frac{\alpha}{2} = \frac{1-\cos \alpha}{2} $
- $ \displaystyle \cos^2 \frac{\alpha}{2} = \frac{1+\cos \alpha}{2} $
- $ \displaystyle \tan^2 \frac{\alpha}{2} = \frac{1-\cos \alpha}{1+\cos \alpha} $
1의 증명
$\begin{aligned}
\sin 2 \alpha &= \sin ( \alpha + \alpha ) = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha \\
&= 2 \sin \alpha \cos \alpha
\end{aligned}$
2의 증명
$\begin{aligned}
\cos 2 \alpha &= \cos ( \alpha + \alpha ) = \cos \alpha \cos \alpha - \sin \alpha \sin \alpha \\
&= \cos^2 \alpha - \sin^2 \alpha \\
&= 2 \cos^2 \alpha -1 \ \ \ ( \because \ \ \sin^2 \alpha = 1 - \cos^2 \alpha ) \\
&= 1-2 \sin^2 \alpha \ \ \ ( \because \ \ \cos^2 \alpha = 1 - \sin^2 \alpha )
\end{aligned}$
3의 증명
$\begin{aligned}
\tan 2 \alpha &= \tan ( \alpha + \alpha ) = \frac{\tan \alpha + \tan \alpha}{1-\tan \alpha \tan \alpha} \\
&= \frac{2 \tan \alpha}{1-\tan^2 \alpha}
\end{aligned}$
4의 증명
$ \cos \alpha = \cos \left( 2 \times \dfrac{\alpha}{2} \right) = 1 - 2 \sin^2 \dfrac{\alpha}{2} $
$ \displaystyle \therefore \ \ \ \sin^2 \frac{\alpha}{2} = \frac{1-\cos \alpha}{2} $
5의 증명
$ \cos \alpha = \cos \left( 2 \times \dfrac{\alpha}{2} \right) = 2 \cos^2 \dfrac{\alpha}{2} - 1 $
$ \displaystyle \therefore \ \ \ \cos^2 \frac{\alpha}{2} = \frac{1+\cos \alpha}{2} $
6의 증명
$ \displaystyle \tan^2 \frac{\alpha}{2} = \frac{\sin^2 \dfrac{\alpha}{2}}{\cos^2 \dfrac{\alpha}{2}} = \frac{\dfrac{1-\cos \alpha}{2}}{\dfrac{1+\cos \alpha}{2}} = \frac{1-\cos \alpha}{1+\cos \alpha} $