수학 공식 | 고등학교 > 정규분포의 뜻과 성질
확률밀도함수
연속확률변수 $ X $가 구간 $ [ \alpha, \ \beta] $에 속하는 모든 실수값을 취하고
\begin{gather*}
{P}(a \leq {X} \leq b) = \int_{a}^{b} f(x) dx \ \ (\alpha \leq a \leq b \leq \beta )
\end{gather*}
와 같이 나타낼 수 있을 때, 함수 $ f(x) $를 연속확률변수 $ X $의 확률밀도함수라고 한다.
확률밀도함수의 성질
연속확률변수 $ X $의 확률밀도함수 $ f(x) \ (\alpha \leq x \leq \beta) $는 다음과 같은 성질을 가진다.
- $ f(x) \geq 0 \ \ (\alpha \leq x \leq \beta) $
- $ \displaystyle \int_{\alpha}^{\beta} f(x) dx = 1 $
- $ \displaystyle {P}(a \leq {X} \leq b) = \int_{a}^{b} f(x) dx \ \ (\alpha \leq a \leq b \leq \beta ) $
정규분포
연속확률변수 $ X $의 확률밀도함수 $ f(x) $가
\begin{gather*}
f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x-m)^2}{2\sigma^2}}
\end{gather*}
일 때, 이 확률분포를 정규분포라 하고, $ {N}(m, \ \sigma^2) $으로 나타낸다.
정규분포곡선의 성질
평균이 $ m $, 표준편차가 $ \sigma $인 정규분포를 따르는 연속확률변수 $ X $의 확률밀도함수 $ f(x) $의 그래프를 정규분포곡선이라고 한다. 정규분포곡선은 다음과 같은 성질을 가지고 있다.
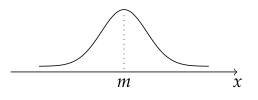
- 직선 $ x=m $ 에 대하여 대칭이고 종 모양의 곡선이다.
- 곡선과 $ x $축 사이의 넓이는 $ 1 $이다.
- $ x $축을 점근선으로 한다.
- $ x=m $일 때, 최댓값을 갖는다.
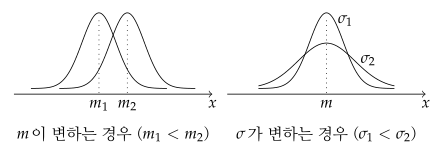
- $ \sigma $의 값이 일정할 때, $ m $의 값이 변하면 대칭축의 위치가 바뀐다.
- $ m $의 값이 일정할 때, $ \sigma $의 값이 커질수록 곡선의 중앙 부분이 낮아지면서 양쪽으로 퍼지고, $ \sigma $의 값이 작아질수록 곡선의 중앙 부분이 높아지면서 좁아진다.
표준정규분포
평균이 $ 0 $, 표준편차가 $ 1 $인 정규분포 $ N(0, \ 1) $을 표준정규분포라 한다.
정규분포의 표준화
- 확률변수 $ X $가 정규분포 $ N (m, \ \sigma^2) $을 따를 때, 확률변수
\begin{gather*}
{Z}=\frac{{X}-m}{\sigma}
\end{gather*}은 표준정규분포 $ N(0, \ 1) $을 따른다. - 확률변수 $ X $를 표준정규분포 $ N(0 , \ 1) $ 을 따르는 확률변수 $ Z $로 변환하는 것을 표준화한다고 한다.
- $ \mathrm{P}( a \leq X \leq b ) = \mathrm{P} \left( \dfrac{a-m}{\sigma} \leq Z \leq \dfrac{b-m}{\sigma} \right) $
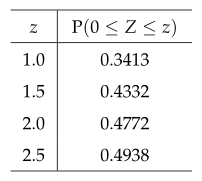
확률변수 $ X $가 정규분포 $ N (10, \ 2^2 ) $을 따를 때, 표준정규분포표를 이용하여 다음 확률을 구하여라.
- $ \mathrm{P}( 12 \leq X \leq 14 ) $
- $ \mathrm{P}( 6 \leq X \leq 12 ) $
- $ \mathrm{P} \left( \dfrac{12-10}{2} \leq Z \leq \dfrac{14-10}{2} \right) = \mathrm{P}( 1 \leq Z \leq 2 ) \\ = 0.4772-0.3413 = 0.1359 $
- $ \mathrm{P} \left( \dfrac{6-10}{2} \leq Z \leq \dfrac{12-10}{2} \right) = \mathrm{P}( -2 \leq Z \leq 1 ) \\ = 0.4772 + 0.3413 = 0.8185 $
이항분포와 정규분포
확률변수 $ X $가 이항분포 $ {B}(n, \ p) $를 따를 때, $ n $이 충분히 크면 $ X $의 분포는 근사적으로 정규분포 $ {N}(np, \ npq) $를 따른다. (단, $ p+q=1 $)
A전자 전체 직원 중에서 $ 80 $\%가 남자라고 한다. 이 회사 직원 중 $ 100 $명을 임의추출할 때, 남자가 $ 88 $명 이상일 확률을 표준정규분포표를 이용하여 구하여라.

남자의 수를 확률변수 $ X $라 하면 $ X $는 이항분포 $ B(100, \ 0.8) $을 따른다. 정규분포로 바꾸면 $ N(80, \ 4^2) $이므로
\begin{gather*}
\mathrm{P} ( X \geq 88 ) = \mathrm{P} \left( Z \geq \frac{88-80}{4} \right) = \mathrm{P} ( Z \geq 2 ) = 0.0228
\end{gather*}