MATH FACTORY

이계도함수를 갖는 함수 $ f(x) $에 대하여 $ f'(a)=0 $일 때

1. $ f''(a) < 0 $이면 $ f(x) $는 $ x=a $에서 극대이다.
2. $ f''(a) > 0 $이면 $ f(x) $는 $ x=a $에서 극소이다.

어떤 구간에서 곡선 $ y=f(x) $ 위의 임의의 두 점 $ P $, $ Q $에 대하여 이 두 점 사이의 곡선 부분이

1. 선분 $ PQ $보다 항상 아래쪽에 있으면, 곡선 $ y=f(x) $는 이 구간에서 아래로 볼록(또는 위로 오목)하다고 한다.
2. 선분 $ PQ $보다 항상 위쪽에 있으면, 곡선 $ y=f(x) $는 이 구간에서 위로 볼록(또는 아래로 오목)하다고 한다.

이계도함수를 갖는 함수 $ y = f(x) $에 대하여 어떤 구간에서

1. $ f''(x) > 0 $이면 곡선 $ y=f(x) $는 이 구간에서 아래로 볼록(또는 위로 오목)하다.
2. $ f''(x) < 0 $이면 곡선 $ y=f(x) $는 이 구간에서 위로 볼록(또는 아래로 오목)하다.

곡선 $ y = f(x) $ 위의 점 $ P(a, \ f(a)) $에 대하여 $ x=a $의 좌우에서 곡선의 모양이 아래로 볼록에서 위로 볼록으로 바뀌거나 위로 볼록에서 아래로 볼로으로 바뀔 때, 이 점 $ P $를 곡선 $ y = f(x) $의 변곡점이라고 한다.

함수 $ y = f(x) $에 대하여

1. $ f''(a) = 0 $이고
2. $ x=a $ 좌우에서 $ f''(x) $의 부호가 바뀌면

점 $ (a, \ f(a)) $는 곡선 $ y=f(x) $의 변곡점이다.

함수 $ y=f(x) $의 그래프의 개형은 다음을 조사하여 그린다.

1. 함수의 정의역과 치역
2. 그래프의 대칭성과 주기
3. 좌표축과의 교점
4. 도함수를 이용한 함수의 증가와 감소, 극대와 극소
5. 이계도함수를 이용한 곡선의 오목과 볼록, 변곡점
6. $ \displaystyle \lim_{x \rightarrow \infty} f(x) $, $ \displaystyle \lim_{x \rightarrow -\infty} f(x) $, 점근선

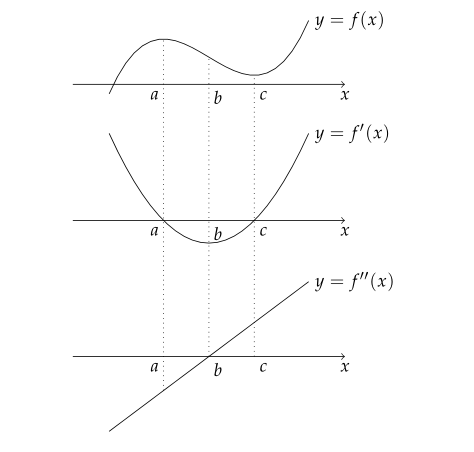
• $ f'(a) = 0 $, $ f''(a) < 0 $이므로 $ x=a $에서 극대
• $ f'(c) = 0 $, $ f''(c) > 0 $이므로 $ x=a $에서 극소
• $ f''(b) = 0 $이고 좌우에서 부호가 바뀌므로 $ x=b $에서 변곡점
• $ x < b $일 때 $ f''(x) < 0 $이므로 위로 볼록
• $ x > b $일 때 $ f''(x) > 0 $이므로 아래로 볼록