수학 공식 | 고등학교 > 적분과 넓이
좌표축과 곡선으로 둘러싸인 부분의 넓이
구간 $ [a, \ b] $에서 곡선 $ y=f(x) $와 $ x $축 사이의 넓이는
\begin{gather*}
\int_{a}^{b} |f(x)| dx
\end{gather*}
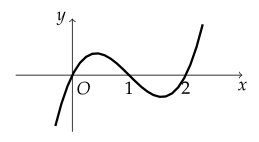
곡선 $ y = x^3 - 3x^2 + 2x $와 $ x $축으로 둘러싸인 부분의 넓이를 구하여라.
곡선과 $ x $축의 교점의 $ x $좌표를 구하면
\begin{gather*}
x^3 - 3x^2 + 2x = 0 \ \ \ \therefore \ \ x = 0 \ 또는 \ 1 \ 또는 \ 2
\end{gather*}
넓이는
\begin{gather*}
\int_{0}^{1} (x^3 - 3x^2 + 2x) dx + \int_{1}^{2} ( - x^3 + 3x^2 - 2x) dx = \frac{1}{2}
\end{gather*}
곡선과 곡선으로 둘러싸인 부분의 넓이
구간 $ [a, \ b] $에서 곡선 $ y=f(x) $와 $ y=g(x) $로 둘러싸인 도형의 넓이는
\begin{align*}
\int_{a}^{b} |f(x)-g(x)| dx
\end{align*}
두 곡선 $ y = - x^2 + 4x - 3 $, $ y = x^2 - 2x + 1 $로 둘러싸인 부분의 넓이를 구하여라.
두 곡선의 교점의 $ x $좌표는
\begin{gather*}
y = - x^2 + 4x - 3, \ y = x^2 - 2x + 1 \ \ \ \therefore \ \ x=1 \ 또는 \ 2
\end{gather*}
넓이는
\begin{gather*}
\int_{1}^{2} \{ ( - x^2 + 4x - 3 ) - (x^2 - 2x + 1) \} dx = \frac{1}{3}
\end{gather*}
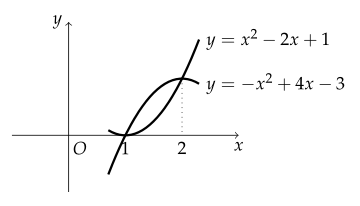
잡동사니
- 구간 $ [a, \ b] $에서 곡선 $ x=f(y) $와 $ y $축 사이의 넓이는
\begin{gather*}
\int_{a}^{b} |f(y)| dy
\end{gather*} - 구간 $ [a, \ b] $에서 곡선 $ x=f(y) $와 $ x=g(y) $로 둘러싸인 도형의 넓이는
\begin{align*}
\int_{a}^{b} |f(y)-g(y)| dy
\end{align*} - $ \alpha < \beta $일 때
\begin{gather*}
\int_{\alpha}^{\beta} |a(x-\alpha)(x-\beta)| dx = \frac{|a|}{6}(\beta-\alpha)^3
\end{gather*} - $ \alpha < \beta $일 때
\begin{gather*}
\int_{\alpha}^{\beta} |a(x-\alpha)^2 (x-\beta)| dx = \frac{|a|}{12}(\beta-\alpha)^4 \\
\int_{\alpha}^{\beta} |a(x-\alpha) (x-\beta)^2| dx = \frac{|a|}{12}(\beta-\alpha)^4
\end{gather*}