수학 공식 | 고등학교 > 함수의 그래프
함수의 그래프의 개형
미분가능한 함수 $ y=f(x) $의 그래프의 개형은 다음과 같은 순서로 그린다.
- 도함수 $ f'(x) $를 구한다.
- 극값이 존재하면 극값을 구한다.
- $ x $의 값에 따른 $ f'(x) $의 부호를 조사한다.
- $ x $절편과 $ y $절편을 구한다.
- 위에서 구한 자료를 이용하여 그래프의 개형을 그린다.
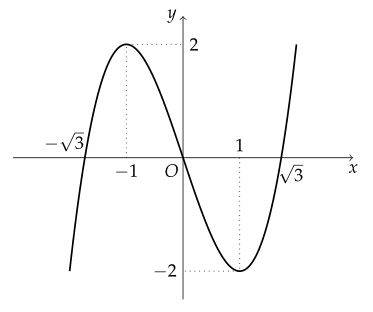
함수 $ f(x) = x^3 - 3x $의 그래프의 개형을 그려라.
$ f'(x) = 3x^2 - 3 = 3(x+1)(x-1) $
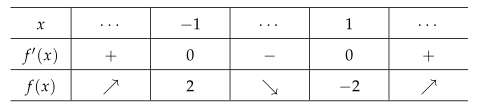
$ x $절편은 $ \pm \sqrt{3}, \ 0 $, $ y $절편은 $ 0 $이다.
함수의 최대와 최소
함수 $ f(x) $가 닫힌 구간 $ [a, \ b] $에서 연속일 때, 극댓값, 극솟값, $ f(a) $, $ f(b) $ 중에서 가장 큰 값이 최댓값, 가장 작은 값이 최솟값이다.
2018/07/15 14:23수학 공식