수학 공식 | 고등학교 > 다항식의 곱셈과 나눗셈
다항식의 곱셈
분배법칙과 지수법칙을 이용하여 전개한 다음 동류항끼리 모아서 정리한다.
다항식의 곱셈에 대한 성질
다항식 $ A $, $ B $, $ C $에 대하여 다음의 연산법칙이 성립한다.
- 교환법칙 : $ AB = BA $
- 결합법칙 : $ (AB)C=A(BC) $
- 분배법칙 : $ A ( B + C ) = AB + AC $, $ ( B + C ) A = BA + CA $
곱셈 공식
- $ (a+b)^2 = a^2 + 2ab + b^2 $
- $ (a-b)^2 = a^2 - 2ab + b^2 $
- $ (a+b)(a-b) = a^2-b^2 $
- $ (x+a)(x+b) = x^2 + (a+b)x + ab $
- $ (ax+b)(cx+d) = acx^2 + (ad+bc)x + bd $
- $ (x+a)(x+b)(x+c) = x^3 + (a+b+c)x^2 + (ab+bc+ca)x + abc $
- $ (a+b+c)^2 = a^2+b^2+c^2+2ab+2bc+2ca $
- $ (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 $
- $ (a-b)^3 = a^3 - 3a^2b + 3ab^2 - b^3 $
- $ (a+b)(a^2-ab+b^2) = a^3+b^3 $
- $ (a-b)(a^2+ab+b^2) = a^3-b^3 $
- $ (a+b+c)(a^2+b^2+c^2-ab-bc-ca) = a^3+b^3+c^3-3abc $
- $ (a^2+ab+b^2)(a^2-ab+b^2) = a^4+a^2b^2+b^4 $
곱셈 공식의 변형
- $ a^2 + b^2 = ( a+b )^2 - 2ab = ( a-b )^2 + 2ab $
- $ (a+b)^2 = (a-b)^2 + 4ab $
- $ a^3 + b^3 = (a+b)^3 - 3ab(a+b) $
- $ a^3 - b^3 = (a-b)^3 + 3ab(a-b) $
- $ a^2 + b^2 + c^2 = (a+b+c)^2 - 2(ab+bc+ca) $
- $ a^3 + b^3 + c^3 = (a+b+c)(a^2 + b^2 + c^2 - ab - bc - ca)+3abc $
- $ a^2 + b^2 + c^2 + ab + bc + ca = \dfrac{1}{2} \left\{ (a+b)^2 + (b+c)^2 + (c+a)^2 \right\} $
- $ a^2 + b^2 + c^2 - ab - bc - ca = \dfrac{1}{2} \left\{ (a-b)^2 + (b-c)^2 + (c-a)^2 \right\} $
다항식의 나눗셈
- 다항식을 다항식으로 나눌 때에는 두 다항식을 내림차순으로 정리한 후 자연수의 나눗셈과 같은 방법으로 계산하여 몫과 나머지를 구한다.
- $ x $에 대한 다항식 $ f(x) $를 $ g(x) $로 나눈 몫을 $ Q(x) $, 나머지를 $ R(x) $라 하면
\begin{gather*}
f(x) = g(x)Q(x) + R(x)
\end{gather*}이다. $ R(x) $의 차수는 $ Q(x) $의 차수보다 낮으며, $ R(x) = 0 $일 때 $ f(x) $는 $ g(x) $로 나누어 떨어진다고 한다.
다항식 $ x^3 + x^2 - 5x + 4 $를 $ x^2 + 2x - 2 $로 나누었을 때의 몫과 나머지를 구하여라.
몫은 $ x-1 $, 나머지는 $ -x+2 $이다.
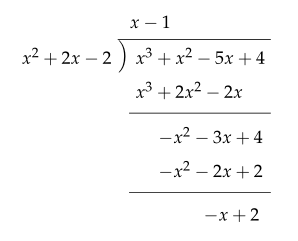
조립제법
다항식을 일차식으로 나눌 때, 계수와 상수항을 이용하여 몫과 나머지를 구하는 방법을 조립제법이라고 한다.
다항식 $ 2x^3 - 5x^2 + 6 $을 일차식 $ x-2 $로 나눈 몫과 나머지를 구하여라.
몫은 $ 2x^2 - x - 2 $, 나머지는 $ 2 $이다.
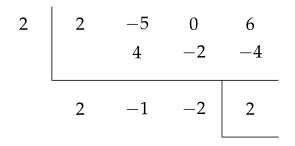
2018/04/25 01:24수학 공식