수학 공식 | 중학교 > 최대공약수와 최소공배수
공약수와 최대공약수
- 두 개 이상의 자연수의 공통인 약수를 공약수라 한다.
- 공약수 중에서 가장 큰 수를 최대공약수라 한다.
- 공약수는 최대공약수의 약수이다.
$ 30 $과 $ 24 $의 최대공약수를 구하여라.
소인수분해를 이용하는 방법
\begin{align*}
30 &= 2 \times 3 \times 5 \\
24 &= 2^3 \times 3 \\
(최대공약수) &= 2 \times 3 = 6
\end{align*}
나눗셈을 이용하는 방법
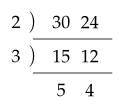
$ (최대공약수) = 2 \times 3 = 6 $
$ 20 $, $ 24 $, $ 36 $의 최대공약수를 구하여라.
소인수분해를 이용하는 방법
\begin{align*}
20 &= 2^2 \ \ \ \ \ \ \ \times 5 \\
24 &= 2^3 \times 3 \\
36 &= 2^2 \times 3^2 \\
(최대공약수) &= 2^2 = 4
\end{align*}
나눗셈을 이용하는 방법
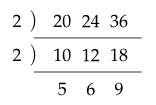
$ (최대공약수) = 2 \times 2 = 4 $
서로소
최대공약수가 $ 1 $인 두 자연수를 서로소라고 한다.
공배수와 최소공배수
- 두 개 이상의 자연수의 공통인 배수를 공배수라 한다.
- 공배수 중에서 가장 작은 수를 최소공배수라 한다.
- 공배수는 최소공배수의 배수이다.
$ 30 $과 $ 24 $의 최소공배수를 구하여라.
소인수분해를 이용하는 방법
\begin{align*}
30 &= 2 \times 3 \times 5 \\
24 &= 2^3 \times 3 \\
(최소공배수) &= 2^3 \times 3 \times 5 = 120
\end{align*}
나눗셈을 이용하는 방법
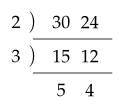
$ (최대공약수) = 2 \times 3 \times 5 \times 4 = 120 $
$ 20 $, $ 24 $, $ 36 $의 최소공배수를 구하여라.
소인수분해를 이용하는 방법
\begin{align*}
20 &= 2^2 \ \ \ \ \ \ \ \times 5 \\
24 &= 2^3 \times 3 \\
36 &= 2^2 \times 3^2 \\
(최대공약수) &= 2^3 \times 3^2 \times 5 = 360
\end{align*}
나눗셈을 이용하는 방법
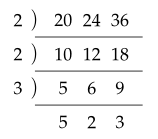
$ (최소공배수) = 2 \times 2 \times 3 \times 5 \times 2 \times 3 = 360 $
세 수의 최소공배수를 구할 때는 어떤 두 수를 택하여도 서로소일 때까지 나눈다.
잡동사니
두 자연수 $ A $, $ B $의 최대공약수를 $ G $, 최소공배수를 $ L $이라 하면
\begin{gather*}
A \times B = L \times G
\end{gather*}
두 자연수의 곱이 $ 720 $, 최소공배수가 $ 120 $일 때, 두 자연수의 최대공약수를 구하여라.
$ 120 \times G = 720 \ \ \ \therefore \ \ G = 6 $