수학 공식 | 고등학교 > 벡터의 뜻과 연산
벡터의 정의
크기와 방향을 가지는 양을 벡터(vector)라 한다. 점 $ {A} $에서 점 $ {B} $로 향하는 벡터가 있다고 할 때, 점 $ {A} $를 시점, 점 $ {B} $를 종점이라 하고, 기호로 $ \overrightarrow{{AB}} $와 같이 나타낸다.
벡터의 크기
벡터의 길이를 벡터의 크기라 하고, $ \overrightarrow{{AB}} $의 크기는 기호로 $ | \overrightarrow{{AB}} | $와 같이 나타낸다. 특히 길이가 $ 1 $인 벡터를 단위벡터, 크기가 $ 0 $인 벡터를 영벡터라 하고 $ \overrightarrow{0} $로 나타낸다.
방향이 반대인 벡터
벡터 $ \overrightarrow{a} $와 크기가 같고 방향이 반대인 벡터를
\begin{gather*}
- \overrightarrow{a}
\end{gather*}
와 같이 나타낸다. 즉,
\begin{gather*}
- \overrightarrow{AB} = \overrightarrow{BA}
\end{gather*}
벡터의 상등
두 벡터가 있을 때 위치에 관계없이 크기와 방향이 같으면 두 벡터는 같다고 한다.
벡터의 덧셈
$ \overrightarrow{a} $의 종점과 $ \overrightarrow{b} $의 시점을 일치시켰을 때, $ \overrightarrow{a} $의 시점을 시점으로, $ \overrightarrow{b} $의 종점을 종점으로 하는 벡터를 $ \overrightarrow{a} $와 $ \overrightarrow{b} $의 합이라 하고, $ \overrightarrow{a} + \overrightarrow{b} $로 나타낸다.
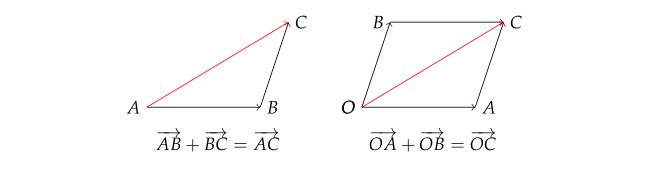
벡터의 덧셈에 대한 성질
- $ \overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a} $
- $ (\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c}) $
- $ \overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a} $
- $ \overrightarrow{a}+(-\overrightarrow{a})=(-\overrightarrow{a})+\overrightarrow{a}=\overrightarrow{0} $
벡터의 뺄셈
두 벡터 $ \overrightarrow{a} $, $ \overrightarrow{b} $에 대하여 $ \overrightarrow{b} + \overrightarrow{x} = \overrightarrow{a} $를 만족하는 $ \overrightarrow{x} $를 $ \overrightarrow{a} $에서 $ \overrightarrow{b} $를 뺀 차라고 하고 $ \overrightarrow{a} - \overrightarrow{b} $로 나타낸다.
벡터의 실수배
실수 $ m $과 벡터 $ \overrightarrow{a} $의 곱 $ m \overrightarrow{a} $은
- $ m > 0 $이면 $ \overrightarrow{a} $와 같은 방향이고 크기가 $ m |\overrightarrow{a}| $인 벡터
- $ m = 0 $이면 영벡터
- $ m < 0 $이면 $ \overrightarrow{a} $와 반대 방향이고 크기가 $ |m| |\overrightarrow{a}| $인 벡터
벡터의 실수배의 성질
임의의 실수 $ m $, $ n $과 벡터 $ \overrightarrow{a} $, $ \overrightarrow{b} $에 대하여
- $ (mn)\overrightarrow{a} = m(n\overrightarrow{a}) = n(m\overrightarrow{a}) =mn\overrightarrow{a} $
- $ (m+n)\overrightarrow{a} = m\overrightarrow{a} + n\overrightarrow{n} $
- $ m (\overrightarrow{a} + \overrightarrow{b}) = m\overrightarrow{a} + n\overrightarrow{b} $
벡터의 상등
$ \overrightarrow{a} \nparallel \overrightarrow{b} $, $ \overrightarrow{a} \neq \overrightarrow{0} $, $ \overrightarrow{b} \neq \overrightarrow{0} $이고 $ m $, $ n $, $ m' $, $ n' $이 실수일 때
- $ m \overrightarrow{a} + n \overrightarrow{b} = \overrightarrow{0} \ \ \Longleftrightarrow \ \ m=0, \ n=0 $
- $ m \overrightarrow{a} + n \overrightarrow{b} = m' \overrightarrow{a} + n' \overrightarrow{b} \ \ \Longleftrightarrow \ \ m=m', \ n=n' $
벡터의 평행조건
영벡터가 아닌 두 벡터 $ \overrightarrow{a} $, $ \overrightarrow{b} $에 대하여
\begin{gather*}
\overrightarrow{a} \parallel \overrightarrow{b} \ \ \Longleftrightarrow \ \ \overrightarrow{b} = k \overrightarrow{a} \ (k \neq 0)
\end{gather*}
세 점 A, B, C가 한 직선 위에 있을 조건
- $ \overrightarrow{{AC}} = k \overrightarrow{{AB}} \ (k \neq 0) $
- $ \overrightarrow{{OC}} = \alpha \overrightarrow{{OA}} + \beta \overrightarrow{{OB}} \ (\alpha+\beta=1) $